THE CHALLENGE
1) Since the CG algorithm deals with large matrices, the problem can easily be bandwidth-bound. Hence, it was essential to store the sparse matrix in a compressed format that does not take up much storage and also enables faster access to reduce element retrieval time.
2) CG is known to converge to the exact solution in N steps for a good-conditioned matrix of size N, which can lead to a lot of computation time for matrices having a very high value of N. Therefore, to reduce this time, the algorithm would be required to stop its iterations much earlier and still obtain a very good approximation after much fewer than N steps. To achieve this, a certain amount of preconditioning is required. An appropriate preconditioner that can produce the fastest convergence under the given code conditions was selected.
3) The algorithm involved many operations like two matrix-vector products, scalar-vector products, etc., all of which are computationally intensive and hence require a lot of time in a single-threaded program.
CAPABILITIES OF OUR CONJUGATE GRADIENT SOLVER
1) Provides a preconditioned sequential implementation of the CG solver
2) Includes a multithreaded implementation of the Preconditioned Conjugate Gradient (PCG) solver using OpenMP primitives
3) Presents a GPU implementation of the PCG using CUDA
INPUT AND OUTPUT CONSTRAINTS
For the linear system Ax = b
Input Constraints
Matrix A must be-
1) Symmetric
2) Positive definite
3) Banded, diagonally heavy
Matrix B must be a vector of size equal to order of A.
Output Constraints
1) Solution x is computed as the result of the algorithm
2) L2 norm of the residual vector must be less than 1e-05 to declare convergence
VISUAL REPRESENTATIONS OF TEST MATRICES USED
| Sr. No. | Test Matrix File Name | Description | N | Non-zero elements |
|---|---|---|---|---|
| 1 | BCSSTK14 | real symmetric positive definite | 1,806 | 63,454 |
| 2 | BCSSTK15 | real symmetric positive definite | 3,948 | 117,816 |
| 3 | BCSSTK18 | real symmetric positive definite | 11,948 | 149,090 |
| 4 | S3DKT3M2 | real symmetric positive definite | 90,449 | 3,753,461 |
| 5 | S3RMT3M3 | real symmetric positive definite | 5,357 | 207,695 |
OUR APPROACH
Compressed Row Storage Format
In order to mitigate the bandwidth-bound problem, we stored the sparse matrices in the compressed row storage format. As per the CRS format, we used three 1-D arrays, such that one array stored only the non-zero elements, the second one stored their corresponding column numbers and the third one gave the row number as well as stored the number at which we index into the other two arrays to retrieve the required element. We observed a reduction in memory storage of about 99.907% for our largest test matrix of size 90449.

Jacobi Preconditioning
As mentioned before, for a good-conditioned matrix, the CG algorithm would converge in N steps. However, for a poor-conditioned matrix A, the same would take even more than N steps for convergence. As a result, preconditioning the matrix is crucial to performance.
Preconditioning is the process of improving the condition number of the matrix A by computing its approximate inverse. Condition number of a function with respect to an argument measures how much the output value X of the function can change for a small change in the input argument i.e. it gives a measure of the sensitivity of the function. The lower the condition number, the better is the preconditioning of the matrix and an ill-conditioned matrix has a high condition number. Therefore, if the condition number is large, even a small error in b may cause a large error in x. On the other hand, if the condition number is small then the error in x will not be much bigger than the error in b.
We implemented three preconditioners, namely, the Symmetric Successive Over-Relaxation, Jacobi and Blocked Jacobi and studied them to obtain the best performing preconditioning. We observed that for our requirements of the matrices (diagonally heavy, banded) the Jacobi preconditioner gave convergence for the lowest number of iterations. Although SSOR is known to precondition the matrix better, our studies showed that it is a strongly serial code due to forward/backward propagations. Therefore, we preconditioned our matrix using the Jacobi preconditioner, since it required the least number of iterations and also had the most scope for parallelization.
Code Profiling
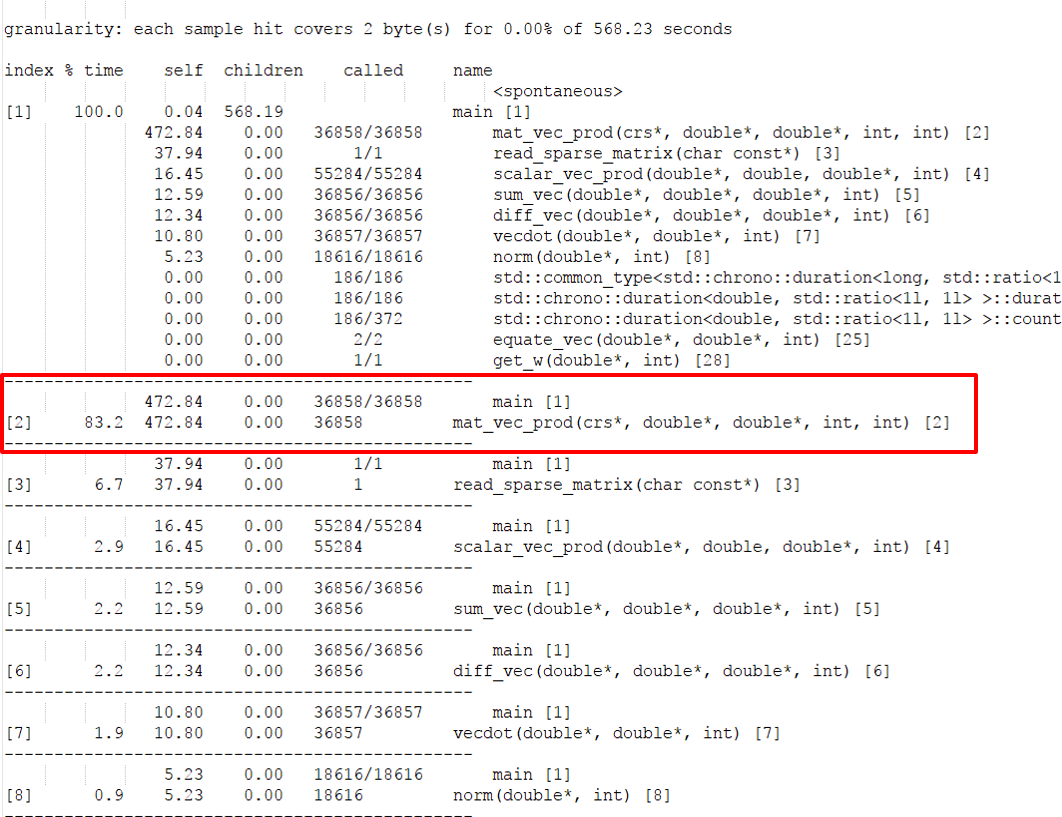
We profiled the sequential code using gprof to determine which functions in our code were taking the most amount of computation time, in order to apply OpenMP primitives or kernalize the function.
Multithreaded implementation using OpenMP
OpenMP (Open Multi-Processing) is an application programming interface (API) that supports multi-platform shared memory multiprocessing programming in C, C++, and Fortran, on most platforms. It consists of a set of compiler directives, library routines, and environment variables that influence run-time behavior.
We profiled our sequential implementation using GNU Gprof which helped us identify the runtime for each section of the program. Most of the time was being spent in Matrix-vector product (over 80%). Hence we decided to optimize the function to compute matrix-vector product efficiently. For this we used openmp pragma “omp parallel for num_threads(nThreads)”.
We also optimized functions to compute the vector dot product using the pragma “omp parallel for reduction num_threads(nThreads)”.
We tested the code against 5 different matrices of different sizes and shapes. We observed that as the workload increases the speedup over the sequential version also increases. This trend can be seen in the speedup graph below.
GPU implementation
CUDA is a parallel computing platform and application programming interface (API) model created by Nvidia. The CUDA platform is designed to work with programming languages such as C, C++, and Fortran.
We created CUDA kernels to perform Matrix-vector on the GPU. For this we split the matrix vector product into three kernels.
1) In the first kernel we compute a nnz sized array of the product of all matrix elements with the corresponding vector elements in parallel. 2) The second kernel was used to compute the inclusive scan on the product array. 3) The third kernel was a gather kernel used to store the appropriate sum into the corresponding position in the result vector.
The inclusive scan step helped us to obtain higher parallelism as opposed to performing reduction on the entire array computed in step 1.
With this we obtained upto 13x speedup over the sequential version.
GRAPHS AND ANALYSIS
1) Improvement in the number of iterations due to Preconditioning
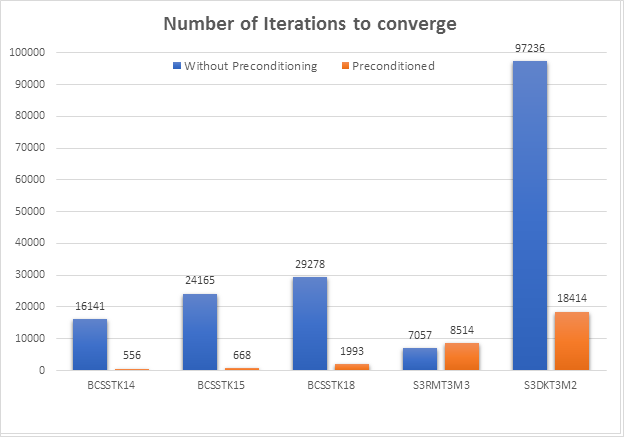
We obtained a significantly huge improvement in the number of iterations required to converge after applying the Jacobi preconditioner. We can see a decrease of over 90% in the number of iterations for convergence for almost all our test matrices except for the S3RMT3M3 matrix. This was the matrix that we had considered as our special test case in order to observe the functioning of our algorithm in cases where the matrix, although sparse, is not diagonally heavy. For this matrix, we observe an increase in the number of iterations. However, all the other matrices perform extremely well, if they fulfil the hard input constraints required by our algorithm.
2) OpenMP vs CUDA
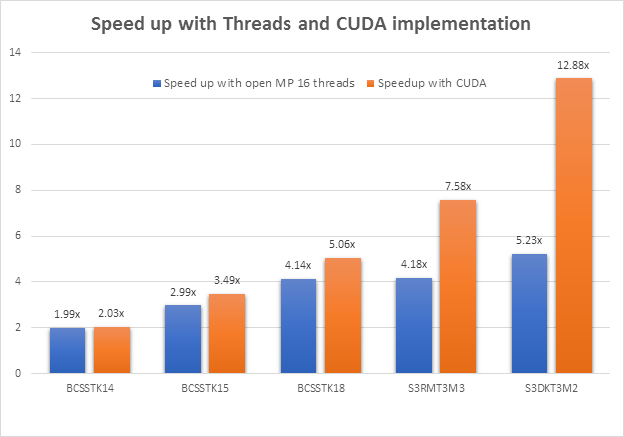
Here, we observed that the speedup for the CUDA implementation of the PCG was always higher than that obtained for the OpenMP implementation. However, for the smaller matrices, the difference is very small. This is because, for smaller matrices, the amount of computation is comparatively lesser and as a result, the overhead of kernel launches cannot be mitigated. Therefore, it becomes comparable to the overhead of spawning threads.
CONCLUSION
1) Compressed row storage is very efficient(upto 99.9% more efficient as compared to the regular matrix storage) for storing sparse matrices, it solved the problem of bandwidth boundedness.
2) Preconditioned CG algorithm converges much faster (upto 30 times faster) as compared to the non preconditioned algorithm.
3) Jacobi Preconditioner, although simple and lightweight, is quite effective in banded and diagonal heavy matrices.
4) Parallelizing matrix vector product on a GPU is effective if the kernel is splitted into product, inclusive scan and gather operations.
RESOURCES
GHC machines: CPU Specs: Xeon E5-1660, 8 cores (2x hyperthreaded), 32GB DRAM
GPU Specs: GeForce GTX1080, 2560-cores, 8GB RAM
WORK DISTRIBUTION
Equal work was performed by both the project members.
REFERENCES
- Michele Benzi, “Preconditioning Techniques for Large Linear Systems: A Survey,” Journal of Computational Physics 182, 418–477 (2002)
- Jonathan Richard Shewchuk, “An Introduction to the Conjugate Gradient Method Without the Agonizing Pain”
- https://www.sharcnet.ca/help/index.php/Solving_Systems_of_Sparse_Linear_Equations
- http://www.idi.ntnu.no/~elster/tdt24/tdt24-f09/cg.pdf
- http://people.sc.fsu.edu/~jburkardt/cpp_src/cg/cg.html
- http://math.nist.gov/MatrixMarket/index.html
- https://en.wikipedia.org/wiki/Sparse_matrix#Solving_sparse_matrix_equations
- https://www.cise.ufl.edu/research/sparse/matrices/
- https://en.wikipedia.org/wiki/Conjugate_gradient_method